共同分岐による濃度低下現象を利用した回転フィルターの開発

旋盤で材料を加工すると加工した際に出た切り粉と切削油が混ざってしまいます。すると切削油の再利用ができません。そこで私達の研究では切削油と切り粉を別々に取り除くことができる回転フィルターの開発をしました。本研究では0.2mmのプラスチック粒子を用いて実験をしました。この回転フィルター装置ができると切削油を再利用ができ、油の消費量も減り環境にも有益です。この回転フィルターの開発は研究室内で10年以上続いている研究で歴代の先輩方が試行錯誤してくださって今の形に到達しました。

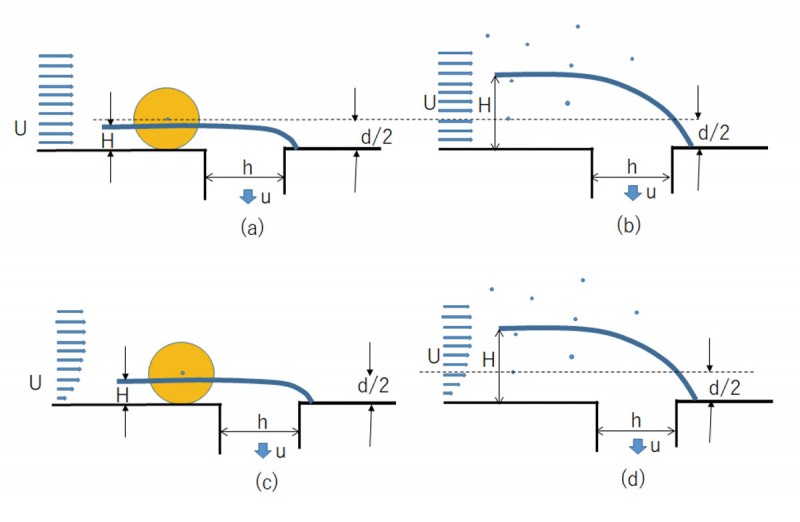
図1は分岐前後の流れを表し、Hは主流における分岐に流入する流体の厚さを、hは分岐流路幅、Uは主流速、uは分岐流路の流速を表す。粒子直径をdとする。(a)は流入厚さHが粒子半径d/2より小さな場合で、粒子は粒子中心の流線に沿って移動すると仮定すると、分岐管に流入する粒子は存在しない。主流の速度分布が壁面まで一様であると仮定すると、(1)となり、ζ を次式で定義すると(2)が、粒子が分岐管に流入しない条件になる。(b)はHがRよりも大きな場合で、速度分布は一様と仮定している。粒子の中心を図示してあるが、壁面からの距離が粒子半径d/2よりも小さな領域には、粒子中心は存在しない。主流路における単位体積中の粒子中心の数をnとすると、分岐管に単位時間に流入する粒子数はn (H-R)Uとなり、分岐管中の単位体積中の粒子数n’は(3)となり、分岐管中の粒子濃度と主流路の粒子濃度の比α_ratioは(4)となる。（ｃ）は境界層厚さが粒子半径よりも大きな場合であり、流入厚さ H が粒子半径 d/2 より小さなくなる場合の分岐流路に流入する流量uhは、境界層の影響でUd/2よりも小さくなるため、(5)となり、分岐流路に粒子が流入しない条件は、ζの値が2よりも大きな値となる必要がある。（ｄ）は境界層厚さならびにＨがRよりも大きな場合であり、流入高さがR以下の粒子を含まない流量が、境界層の影響でUd/2よりも小さくなるために、分岐管中の単位体積中の粒子数n’は(6)となり、分岐管中の粒子濃度と主流路の粒子濃度の比 α_ratioは (7)となって、フィルタリング効果が小さくなる。そこで境界層の厚さを粒子半径に比して、できるだけ薄くする必要がある。

（１）d/2>H=uh/U
（２）ζ＝Ud/uh>2
（３）n’=n (H−R)U/UH=n(1−d/2H)
（４）α_ratio＝n’/n=(1−d/2H)=(1−dU/2uh)=1−ζ/2
（５）Uh<Ud/2 すなわち ζ＝Ud／uh>2
（６）n’＞(nuh−nUd/2)/uh
（７）α_ratio＝n’/n＞1−dU/2uh=1−ζ/2

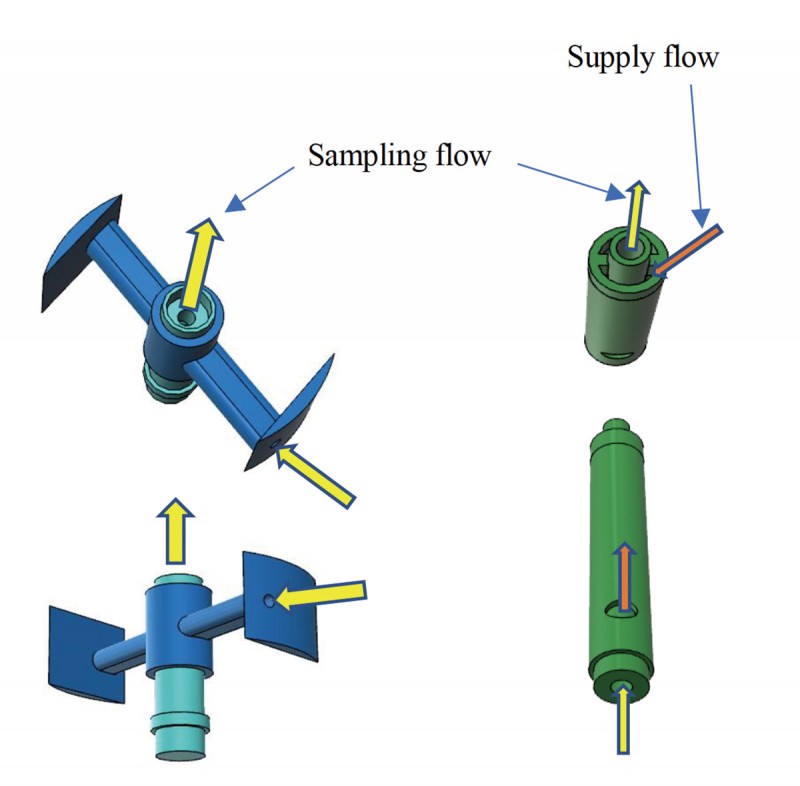
吸入孔の上の速度分布が、壁面まで一様であれば、上記のように濃度低下が起こり、フィルタリング効果を発揮するが、粘性流体であるが故に境界層の影響を考慮する必要がある。吸入孔上の境界層厚さをできるだけ薄くすることと、乱れをできるだけ抑える構造にする必要がある。そこで外円筒回転式とし、外円筒内壁面近くに静止円弧翼を配置して、翼先端からなるべく近い位置に吸入孔を設けた。外円筒内径は約60mmである。図2〜図6に概要を示す。図2（省略）は組み立て図、図3（省略）は回転外円筒、図4は静止円弧翼で先端から5mmの位置に吸入孔を配置した。図5（省略）は中心軸。中央部には静止円弧翼の吸入孔から吸引された流体が上方に向かって流れる穴があり、その周囲にその流量を補うために外部から流体を供給して下方に流れる隙間と流出する穴が設けられている。図4の部品は図5（省略）の部品の下方に接続される。図6は回転外円筒と円弧翼の位置関係を示す。粒子を含んだ液体が中心軸から供給され、回転外円筒によって乱れが少ない強制渦が形成され、静止円弧翼に配置された吸入孔から吸入され、中心軸中央の穴を通り排出される。

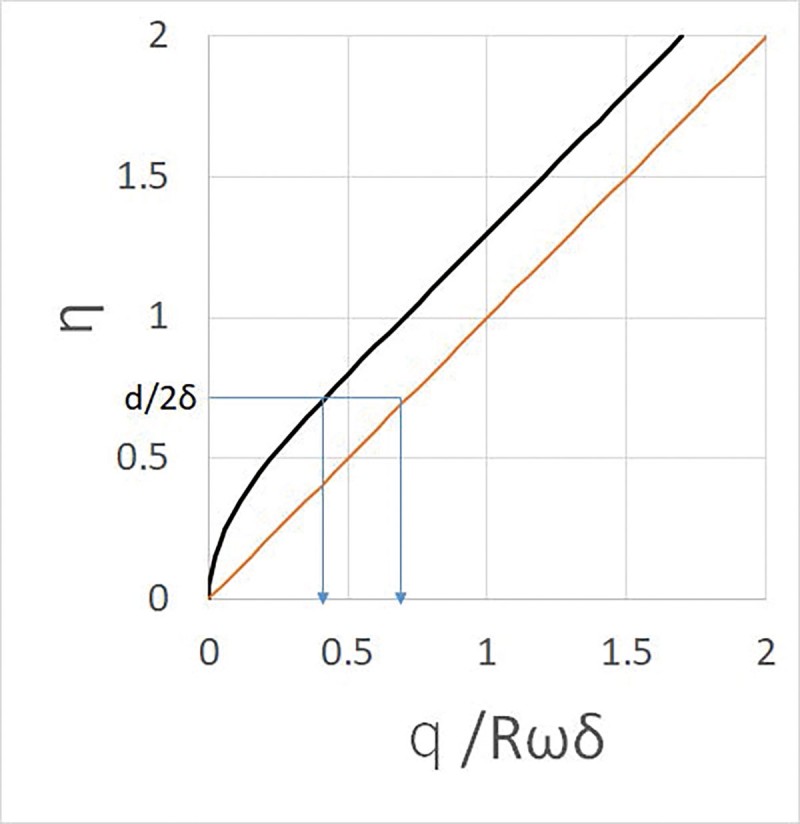
静止円弧翼上のある吸入孔上部の境界層厚さをδ、円弧翼先端から吸入孔の距離をｘ、流体密度と粘度をそれぞれρ、μとすると、二重円筒の角速度をω、吸入孔の容器中心からの距離をRとするととなる。境界層内部の速度分布をη＝y/δを用いて、次式で近似する。η＜1 の場合の単位幅当たりの流量はη＞1 の場合の単位幅当たりの流量はとなる。図7（省略）に速度分布を、図8に流量とηの関係を示す。縦軸はともにηであり、横軸はそれぞれu/Rω，q/Rωδ をとった。図8において直径dの粒子が吸入孔に流入しない流量ｑ_limitは、境界層の存在により減少することがわかる。η_R＝d/2δとすると、となる。境界層の影響を加味したフィルタリング効果は　E_th＝1−(q—q_limit)／q　で与えられる。

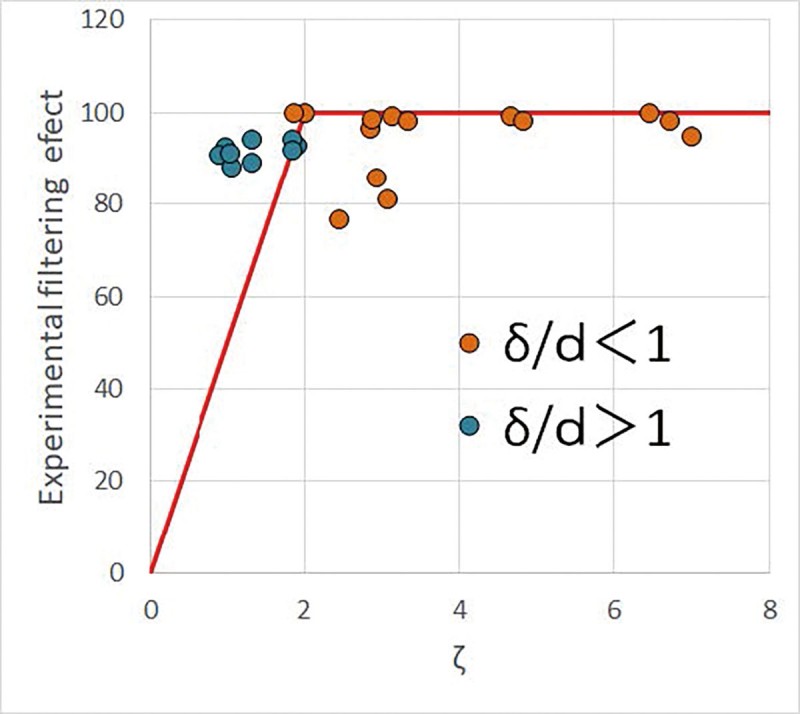
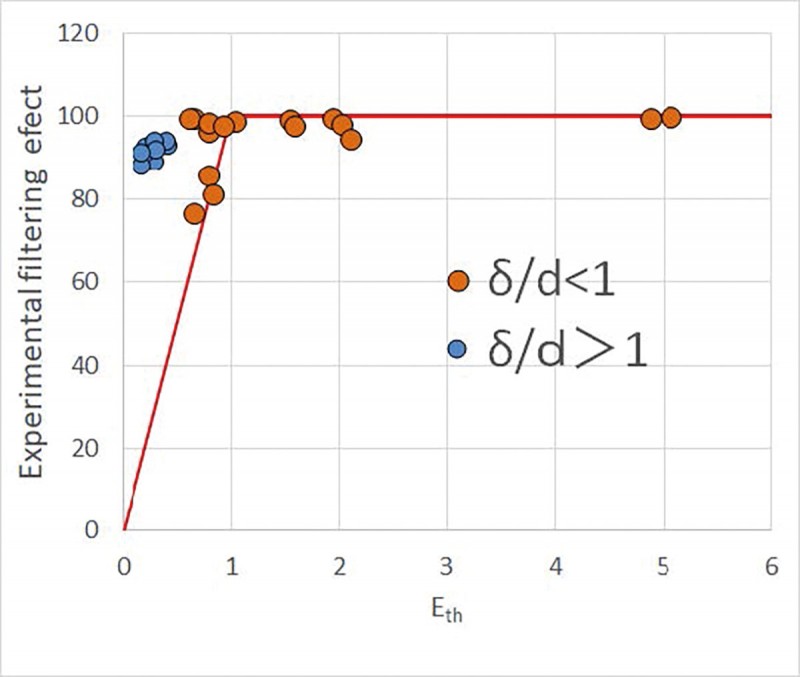
図9（省略）に供試粒子形状を示す。図10は横軸にζ、縦軸にフィルタリング効果をとった。実線が理論値で、赤の実験点は理論線より少し下方に分布している。これは境界層の影響で、フィルタリング効果が減少したと考えられる、図11は縦軸にフィルタリング効果、横軸に境界層を考慮したフィルタリング効果の理論値Ethをとった。実線が理論線である。赤の実験点はほぼ理論線上に分布している。赤の実験点は吸入孔上の境界層の厚さが粒子直径よりも小さな場合である。青の実験点は境界層厚さが粒子直径よりも大きな場合であり、図10、図11ともに理論線よりも上方に位置しており、理論よりもフィルタリング効果が大きいことを意味している。これは境界層内部で、粒子は壁面から離れる動きをすることが知られており、この効果でフィルタリング効果が理論値よりも良くなったと考えられる。

分岐による濃度低下現象を用いた回転フィルターを作成するにあたり、外円筒回転の強制渦にて流れを誘起することにより乱れを抑え、吸入孔上部の境界層の厚さをできる限り小さく、乱れを極力抑えた装置を開発した。0.2mmのプラスチック粒子を、プラスチック粒子と同じ比重に調整した食塩水の中に入れて実験を行った。境界層の速度分布を考慮したフィルタリング効果の理論値と、フィルタリング効果の実験値はほぼ一致した。さらに境界層の厚さが粒子直径よりも大きな場合は理論よりも良いフィルタリング効果があることが確かめられた。これは粒子には境界層内部で壁面から離れる挙動があることによると考えられる。