ステアリングロボットを用いた周波数応答解析システムの構築

自動車の特性を測る試験の一つに操舵入力による周波数応答特性試験がある。周波数応答試験とは操舵入力に対する車両応答の伝達関数を求めるものであり、操舵入力には一般的に三角パルス操舵入力、スイープ操舵入力があり、工業規格において乗用車の操舵過渡応答試験方法に規定されている。本実験では，操舵入力に対して車両応答の出力「ヨーレイト」、「横加速度」のパラメータを計測しフーリエ変換を行い周波数領域に於いてボード線図を描き入出力のゲイン及び位相差を確認した。また、このような操舵を含む車両実験に於いて人間による操舵では繰り返し同一の入力を行うことができず、様々な車種や仕様で比較する際に、操舵に差が生じ純粋な車両の機械的特性をつかむことが難しくなる。そこで本実験ではステアリングロボットを用いて任意の規則性のある波形を入力することにより実車両で正確な解析を可能とした。

実験装置にはAB Dynamics社ステアリングロボットSR15 Orbit、Kistler社ジャイロ内蔵すべり角センサCorrevit S-Motion、DEWE Japan社データロガーSIRIUS/SBOX2を使用し、車両情報はOBD2ポートからCAN信号を取り出し計測した。
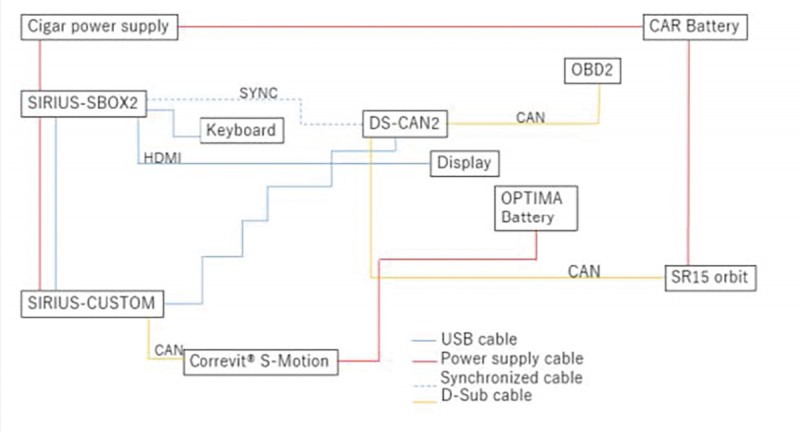
ステアリングロボットでは車両ステアリングに任意の操舵波形を入力し自動操舵を行うことができる。この自動操舵に対する応答として、すべり角センサでは速度、横加速度、ヨーレイトを測定した。測定したデータはデータロガーを使用し、CAN通信によって各計測装置のデータの同期を行い、計測システムを構築した。計測システム全体図をFig.1に示す。

ステアリングロボットで実験を行う上でマニュアルトランスミッション車両ではドライバがステアリング操作、シフト操作を行うため両手が埋まってしまう。また安全上の理由としてステアリングロボットの操作はドライバが起動 スイッチを入力する必要がある。このため起動スイッチをシフトレバーと一体化させた。ステアリングロボット搭載時のレイアウトをFig.2に示す。
実験方法として、車速80Km/hで直進走行し車両を定常状態に保ち、操舵波形を入力しヨーレイト、横加速度および横すべり角をすべり角センサで測定する。測定したデータはフーリエ変換を行いボード線図に描き出し車両の周波数応答解析を行う。
操舵波形は４つの仕様の波形を使用する。

(1)三角波入力
波形はパルス幅0.5(s)振幅60(deg)の波形を入力する。また三角波入力では車両の応答が収まるまで操舵後3秒間ステアリングを直進状態に保ちデータを収集した。
(2)多重正弦波入力  
多重正弦波の基本式を下に示す。
t テストタイム（s）
T 総テストタイム（s）
N 周波数個数
a 振幅（deg） 

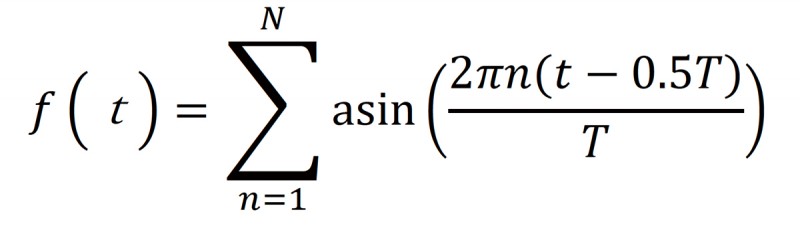
上記の数式を使用し異なる３つの仕様の多重正弦波を作成した。なお基本周波数は全仕様 0.2Hzとして仕様ごとに振幅、周波数を変更した。
多重正弦波（a）
T=0.5(s)、a=0.44(deg)、N=28 振幅 0.44(deg)のサイン波を28個フーリエ級数展開によって足し合わせた。
多重正弦波（b）
T=0.5(s)、a=2.75(deg)、N=15 振幅 2.75(deg)のサイン波を15 個フーリエ級数展開によって足し合わせた。
多重正弦波（c）
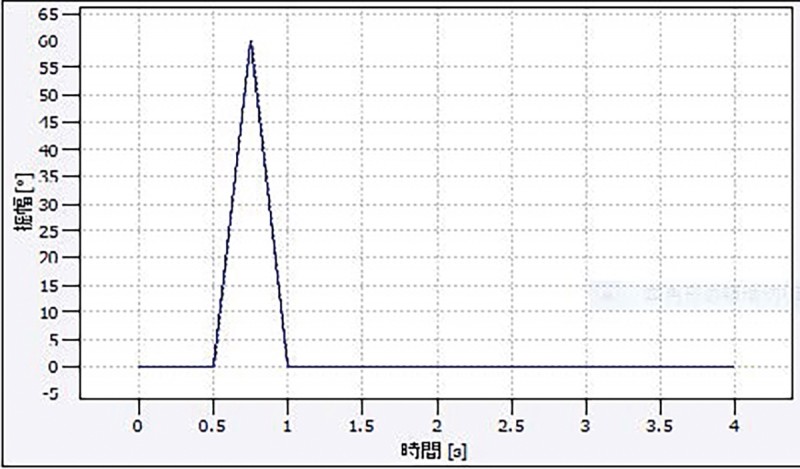
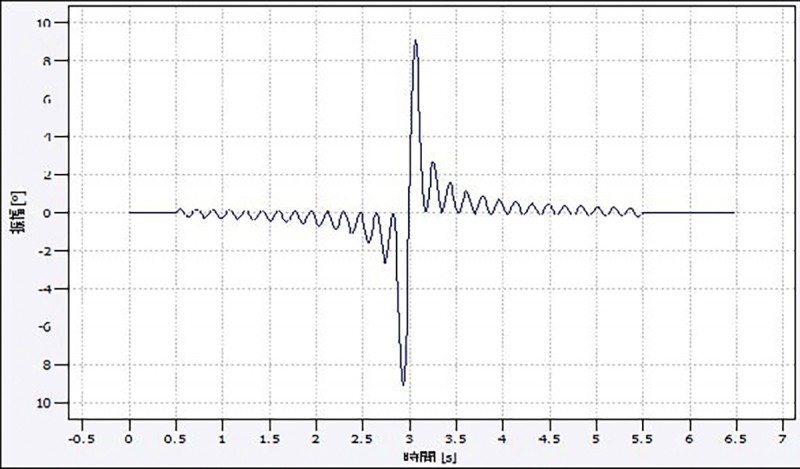
T=0.5(s)、a=8.50(deg)、N=10振幅 8.5(deg)のサイン波を10個フーリエ級数展開によって足し合わせた。三角波、多重正弦波（1）の波形をFig.4 Fig.5に示す。

ボード線図
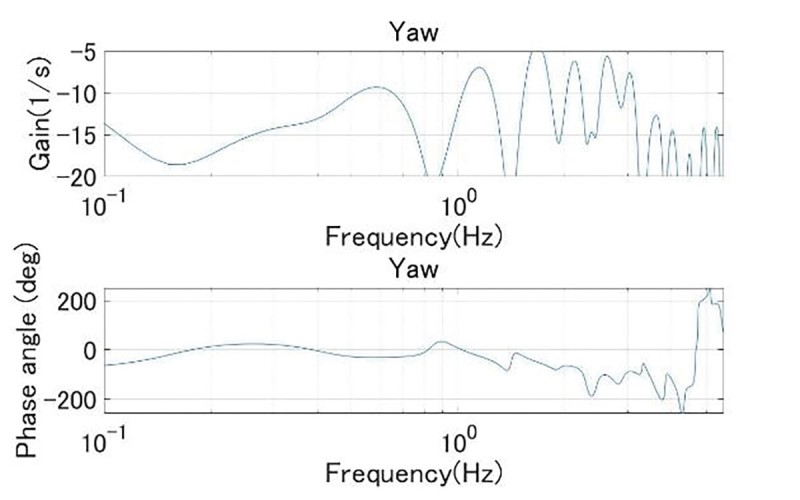
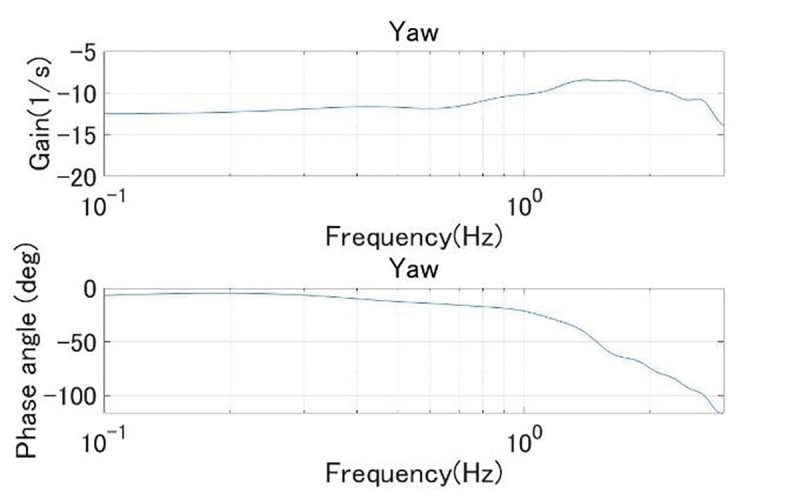
パルス幅0.5s振幅60°のボード線図をFig.6（略）、多重正弦波（a）(b）(c）の各ボード線図をそれぞれFig.7、Fig.8、Fig.9に示す。
三角波入力試験では1.5Hz付近にヨーレイトの振幅比ピークがみられ、徐々に減少していった。このことから実験車両がアンダーステア特性を有していることが分かる。多重正弦波入力試験では（a）の波形において三角波入力と比較して舵角が小さくなったために、ヨーレイト成分が路面状態や横風に影響されノイズに埋もれていることが他の舵角と比較して分かる。また（b）、(c）の波形では低周波数領域に三角波入力との差異がみられる。

ステアリングロボットの操作方法および実車実験におけるデータの収集方法、安全に配慮をした実験手順の確立をした。また、ステアリングロボットの許容する範囲での操舵波形の検討と、それに付随する実験条件等の検討も行い、今後ステアリングロボットを用いた実験の指標となる結果が得られた。