卒業研究のご紹介
2020年版
機械・自動車・ロボット系所属学生
コーストレース制御向上に寄与する リアルタイムな自車位置推定アルゴリズムの研究
關野 修東京都
大学院機械システム工学専攻 博士前期課程 2020年3月修了
(創造工学部自動車システム開発工学科 2018年3月卒業)
(創造工学部自動車システム開発工学科 2018年3月卒業)
日本工業大学駒場高等学校出身
研究の目的
高度運転支援システムおよび自動運転システムには、高精度な自車位置推定技術が求められる。このような技術として、現在では主にLiDARと高精度3D地図を用いたスキャンマッチングや超高精度IMUとGNSSを組み合わせた複合航法システムが挙げられるが、スキャンマッチングは地形や建物の形状によってスキャンマッチングが収束せず自車位置推定が不能になるなどロバスト性の面で課題があったり、連続性が担保されないなどの課題がある。また超高精度IMUを用いた複合航法システムは、非常に高額な方式のIMUを用いたシステムであるため、市販車に搭載することは困難である。
そこで本研究では、廉価で汎用的なMEMS IMUと車輪速センサ、GNSS受信機を組み合わせ、ロバストで高精度かつ、リアルタイム性の高い自車位置推定アルゴリズムの研究を行い、車両制御性能の向上に寄与することを明確にした。
そこで本研究では、廉価で汎用的なMEMS IMUと車輪速センサ、GNSS受信機を組み合わせ、ロバストで高精度かつ、リアルタイム性の高い自車位置推定アルゴリズムの研究を行い、車両制御性能の向上に寄与することを明確にした。
研究内容や成果等
■ 自車位置推定手法
(1)デッドレコニングの課題
デッドレコニングとは、ヨーレイトと車輪速から自車の相対位置を推定することを言う。スキャンマッチングにおける精度とロバスト性の向上やGNSSで推定した自車位置の補間に用いられ、車両制御に対する影響度の高い要素である。しかし長時間デッドレコニングによる位置補間を行うと積分誤差が蓄積され、自車位置推定結果の誤差が増大するという課題がある。
(2)リアルタイム位置推定アルゴリズム
これまで、IMUと車輪速度センサに加えマルチGNSS受信機を組み合わせ、GNSSドップラを活用し高精度な自車位置を推定する手法が提案されている。中でも本研究では、廉価なMEMS IMU、車輪速度センサ、マルチGNSS受信機の組み合わせで、高精度な位置推定を可能にしている手法を実車に適用できるようリアルタイム化を行い、コーストレース制御に適用するための位置推定アルゴリズムを開発する。
(3) GNSSドップラ
GNSSからの情報は主に、ドップラシフト周波数から推定した自車の速度ベクトルである。衛星が航行する速度は既知であるため、4つ以上の衛星から信号を受信できれば、自車の速度ベクトルを算出することが可能である。各速度ベクトルを用いて、式(1)より自車の車速、式(2)より絶対的な方位角を求めることができる。このとき、VN, VE, VU がそれぞれ北、東、高さ方向の速度ベクトル、VD, θD が車速と方位角を示す。
デッドレコニングとは、ヨーレイトと車輪速から自車の相対位置を推定することを言う。スキャンマッチングにおける精度とロバスト性の向上やGNSSで推定した自車位置の補間に用いられ、車両制御に対する影響度の高い要素である。しかし長時間デッドレコニングによる位置補間を行うと積分誤差が蓄積され、自車位置推定結果の誤差が増大するという課題がある。
(2)リアルタイム位置推定アルゴリズム
これまで、IMUと車輪速度センサに加えマルチGNSS受信機を組み合わせ、GNSSドップラを活用し高精度な自車位置を推定する手法が提案されている。中でも本研究では、廉価なMEMS IMU、車輪速度センサ、マルチGNSS受信機の組み合わせで、高精度な位置推定を可能にしている手法を実車に適用できるようリアルタイム化を行い、コーストレース制御に適用するための位置推定アルゴリズムを開発する。
(3) GNSSドップラ
GNSSからの情報は主に、ドップラシフト周波数から推定した自車の速度ベクトルである。衛星が航行する速度は既知であるため、4つ以上の衛星から信号を受信できれば、自車の速度ベクトルを算出することが可能である。各速度ベクトルを用いて、式(1)より自車の車速、式(2)より絶対的な方位角を求めることができる。このとき、VN, VE, VU がそれぞれ北、東、高さ方向の速度ベクトル、VD, θD が車速と方位角を示す。
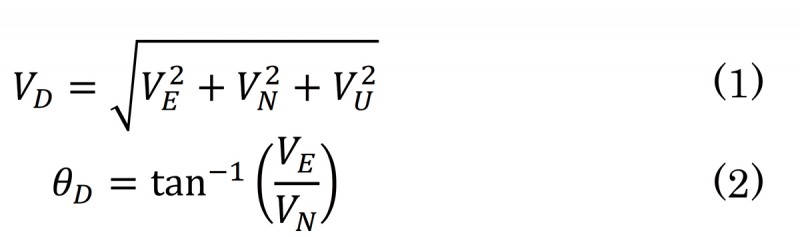
(4)位置推定アルゴリズム概要
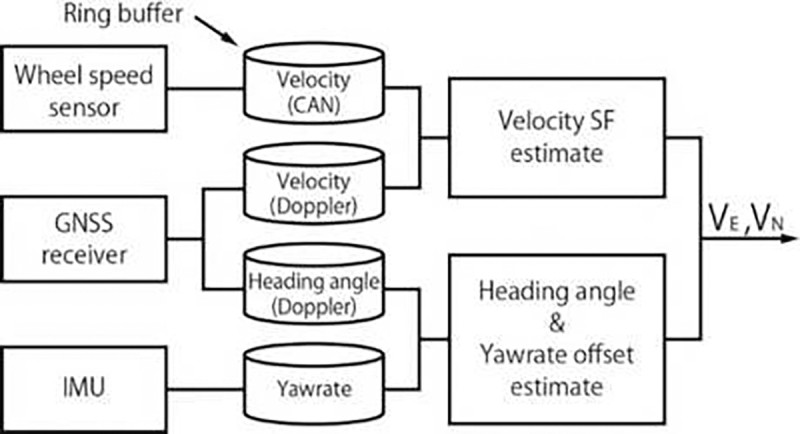
位置推定アルゴリズムは、各種センサから一定時間のデータ蓄積が必要になる。そこでリアルタイム化のため、新たにリングバッファーを実装した。このバッファー内のデータを用いて、各推定値を算出する。
位置推定アルゴリズムは、各種センサから一定時間のデータ蓄積が必要になる。そこでリアルタイム化のため、新たにリングバッファーを実装した。このバッファー内のデータを用いて、各推定値を算出する。
(5)車輪速スケールファクタの推定
車輪速センサから算出される車速情報は、車輪の回転数とタイヤ径から計算されるが、基準に対する実際のタイヤ径の比などから誤差が含まれている。この誤差要因として特に支配的なタイヤ径の比の補正を、本来の車速にかかるスケールファクタSFとすると、実際の車速Vは式(3)のように示される。また、衛星からの信号の受信が良好な場合、GNSSドップラを用いて算出した車速VDが高精度であることが知られている。そのため、衛星の受信状況の良い環境ではVDを実際の車速Vとみなすことができ、SFは式(4)で計算できる。ただし、VDは常に高精度とは限らない上に、SFは動的に変化しない。そこで GNSS受信時かつ、一定車速以上で走行しているデータがバッファーに一定数以上あるときに、そのデータを使用し、データ全体のVDをVCANで除算し、その中央値を車輪速スケールファクタ推定値SFとした。
車輪速センサから算出される車速情報は、車輪の回転数とタイヤ径から計算されるが、基準に対する実際のタイヤ径の比などから誤差が含まれている。この誤差要因として特に支配的なタイヤ径の比の補正を、本来の車速にかかるスケールファクタSFとすると、実際の車速Vは式(3)のように示される。また、衛星からの信号の受信が良好な場合、GNSSドップラを用いて算出した車速VDが高精度であることが知られている。そのため、衛星の受信状況の良い環境ではVDを実際の車速Vとみなすことができ、SFは式(4)で計算できる。ただし、VDは常に高精度とは限らない上に、SFは動的に変化しない。そこで GNSS受信時かつ、一定車速以上で走行しているデータがバッファーに一定数以上あるときに、そのデータを使用し、データ全体のVDをVCANで除算し、その中央値を車輪速スケールファクタ推定値SFとした。
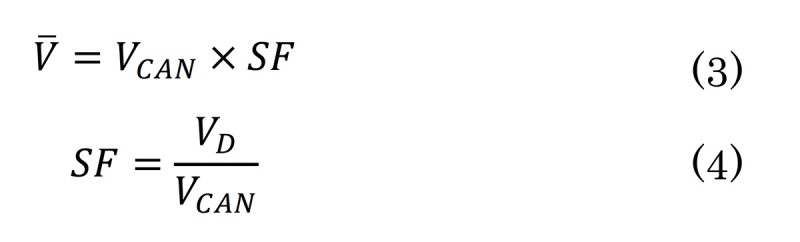
(6)絶対的な方位角の推定
絶対的な方位角の推定には、IMUのヨーレイトを時間積分して算出した方位角θGと、GNSS ドップラを用いて算出した方位角θDを利用する。ここでθGは式(5)により計算する。このとき φ.はIMUから出力されるヨーレイト、Δφはヨーレイトオフセット補正値を示す。Δφ.は後述するヨーレイトオフセット推定より算出した値(停止中は Δφ.S、走行中は Δφ.R)を使用する。バッファー内に、GNSS受信中かつ、一定車速以上、一定ヨーレイト未満のデータが一定数あるとき、そのデータを使用し、推定を行う。
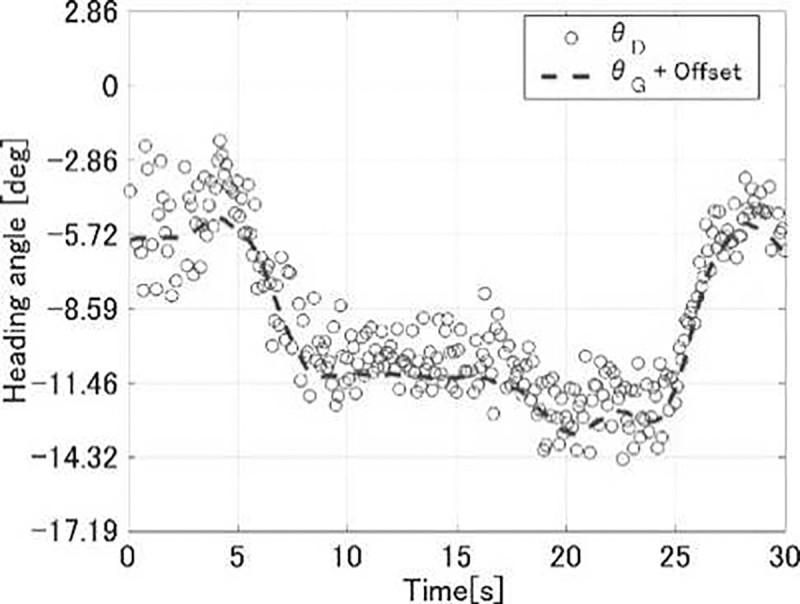
θGは積分開始時を基準として方位角を計算しているので、北を基準とした方位角であるθDとは一定のオフセットがある。このオフセットを現時間tnew(図中ではtnew=30)のデータより式(6)を用いて計算する。式(7)に示すように、データ中のθGをdiffH分オフセットさせると図3のようになる。
その後、式(8)に示すようにデータ全体を、θDを基準にθG offset Hとの差分diff"Hを計算し、この差の平均値を利用して式(12)で暫定の方位角θTを算出する。暫定の方位角θTを用いて再度θGをオフセットさせ、θDとの差分diff"Hを算出する。
ここで、暫定の方位角分オフセットさせたθGとGNSSドップラで求めた方位角θDの差分diff"Hを用いて、マルチパス等の影響などで発生したθDの外れ値を除去する。diff"Hが、ある一定の数値を超えている場合、そのデータを外れ値と見なして除去し、式(6)へ戻る。この処理を外れ値が無くなるまで行い、最終的な暫定の方位角θTを推定した方位角θEとする。
絶対的な方位角の推定には、IMUのヨーレイトを時間積分して算出した方位角θGと、GNSS ドップラを用いて算出した方位角θDを利用する。ここでθGは式(5)により計算する。このとき φ.はIMUから出力されるヨーレイト、Δφはヨーレイトオフセット補正値を示す。Δφ.は後述するヨーレイトオフセット推定より算出した値(停止中は Δφ.S、走行中は Δφ.R)を使用する。バッファー内に、GNSS受信中かつ、一定車速以上、一定ヨーレイト未満のデータが一定数あるとき、そのデータを使用し、推定を行う。
θGは積分開始時を基準として方位角を計算しているので、北を基準とした方位角であるθDとは一定のオフセットがある。このオフセットを現時間tnew(図中ではtnew=30)のデータより式(6)を用いて計算する。式(7)に示すように、データ中のθGをdiffH分オフセットさせると図3のようになる。
その後、式(8)に示すようにデータ全体を、θDを基準にθG offset Hとの差分diff"Hを計算し、この差の平均値を利用して式(12)で暫定の方位角θTを算出する。暫定の方位角θTを用いて再度θGをオフセットさせ、θDとの差分diff"Hを算出する。
ここで、暫定の方位角分オフセットさせたθGとGNSSドップラで求めた方位角θDの差分diff"Hを用いて、マルチパス等の影響などで発生したθDの外れ値を除去する。diff"Hが、ある一定の数値を超えている場合、そのデータを外れ値と見なして除去し、式(6)へ戻る。この処理を外れ値が無くなるまで行い、最終的な暫定の方位角θTを推定した方位角θEとする。
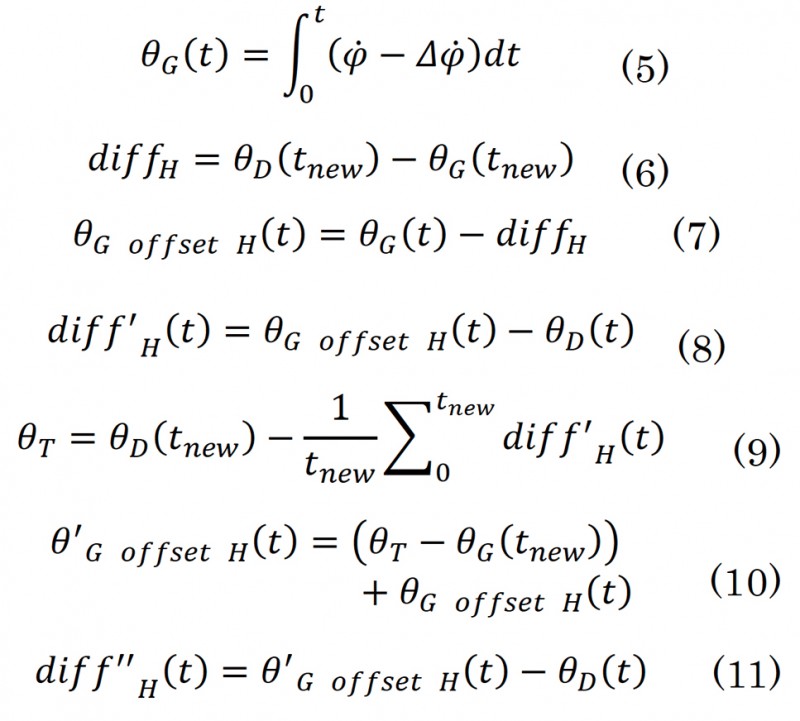
(7)ヨーレイトオフセット値の推定
車両停止中のヨーレイトオフセットの推定は、一般的な手法(5)として用いられている停止中のヨーレイト平均値を使用する。停止中のt秒間(今回はt=4)の平均値を停止時ヨーレイトオフセット推定値φSとした。
走行時のヨーレイトオフセットの推定は、前項で推定した方位角θEとIMUから出力されるヨーレイト φ.を補正せずに、時間積分した値θG RAWを用いて行う。
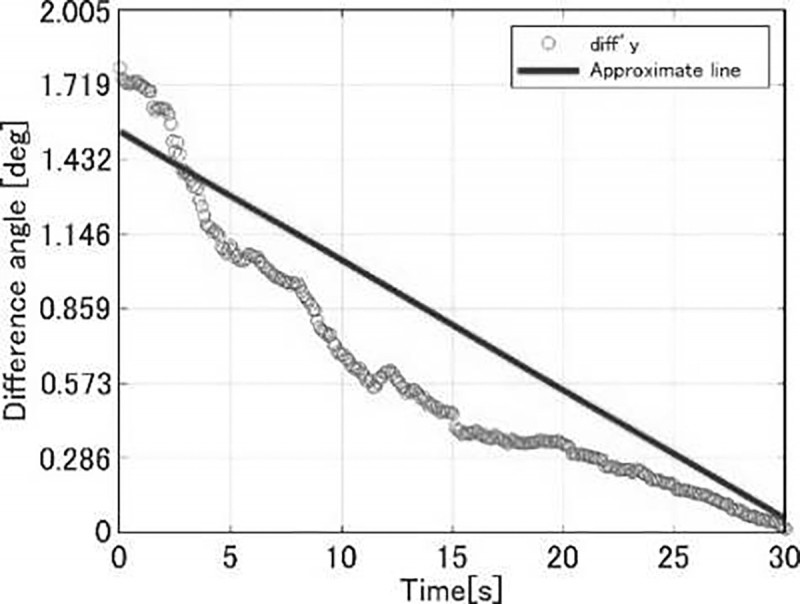
まず式(14)に示すように現時間tnewでのθG rawとのオフセットdiffYを算出する。その後式(15)に示すように、データ中のθG RAWを、diffY分オフセットさせる。このθG RAWをθEに合わせてオフセットさせた値であるθG offset Yと、θEの差分を式(16)に示すように計算する。diff'Y(t)は現時間tnewを基準に、θG RAWをθEに合わせてオフセットさせ、求めた差分であるため、図4からも読み取れるように、過去に遡るほど差分が広がる。この差分の傾きをヨーレイトオフセット値として、最小二乗法で近似直線を求め、その傾きを走行時のヨーレイトオフセット値 φ.Rとした。
車両停止中のヨーレイトオフセットの推定は、一般的な手法(5)として用いられている停止中のヨーレイト平均値を使用する。停止中のt秒間(今回はt=4)の平均値を停止時ヨーレイトオフセット推定値φSとした。
走行時のヨーレイトオフセットの推定は、前項で推定した方位角θEとIMUから出力されるヨーレイト φ.を補正せずに、時間積分した値θG RAWを用いて行う。
まず式(14)に示すように現時間tnewでのθG rawとのオフセットdiffYを算出する。その後式(15)に示すように、データ中のθG RAWを、diffY分オフセットさせる。このθG RAWをθEに合わせてオフセットさせた値であるθG offset Yと、θEの差分を式(16)に示すように計算する。diff'Y(t)は現時間tnewを基準に、θG RAWをθEに合わせてオフセットさせ、求めた差分であるため、図4からも読み取れるように、過去に遡るほど差分が広がる。この差分の傾きをヨーレイトオフセット値として、最小二乗法で近似直線を求め、その傾きを走行時のヨーレイトオフセット値 φ.Rとした。
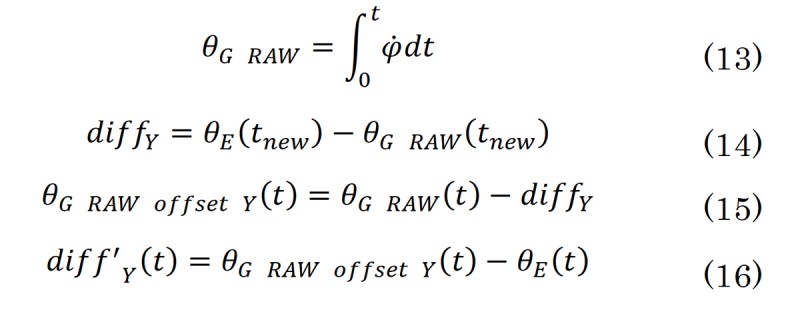
■ 相対位置推定性能評価試験
(1)評価試験概要
自車の相対位置推定性能を評価するため、本評価試験では図5(略)に示す本学周辺道路にて、測量用のRTK-GNSSをリファレンス機として同時計測を行った。
(2)相対位置推定性能の評価
リファレンスから求めた走行軌跡と、本アルゴリズムから推定した補正車速と補正ヨーレイトを用いて求めた走行軌跡、一般的な手法である停止時ヨーレイトオフセット推定のみを行って求めた走行軌跡の3つを用いて相対位置の評価を行った。評価方法として、10mごとに100m走行後のリファレンスとの軌跡の誤差比較を行い、求めた誤差平均を元に走行データ中の誤差の割合を求めた。
結果を図6(略)に示す。横軸がリファレンスとの誤差を表し、縦軸が今回の走行データ全体における誤差の割合を示す。一般的に用いられる手法では100mの走行で2.0m以内の自車位置推定を約95%出来ていたが、本手法では0.6m以内の推定を約95%行うことが出来た。
自車の相対位置推定性能を評価するため、本評価試験では図5(略)に示す本学周辺道路にて、測量用のRTK-GNSSをリファレンス機として同時計測を行った。
(2)相対位置推定性能の評価
リファレンスから求めた走行軌跡と、本アルゴリズムから推定した補正車速と補正ヨーレイトを用いて求めた走行軌跡、一般的な手法である停止時ヨーレイトオフセット推定のみを行って求めた走行軌跡の3つを用いて相対位置の評価を行った。評価方法として、10mごとに100m走行後のリファレンスとの軌跡の誤差比較を行い、求めた誤差平均を元に走行データ中の誤差の割合を求めた。
結果を図6(略)に示す。横軸がリファレンスとの誤差を表し、縦軸が今回の走行データ全体における誤差の割合を示す。一般的に用いられる手法では100mの走行で2.0m以内の自車位置推定を約95%出来ていたが、本手法では0.6m以内の推定を約95%行うことが出来た。
■ 車両制御評価試験
(1)評価試験概要
本アルゴリズムの車両制御適用時の有効性を確認するため、外部ECUから制御を行えるように改造した実験車を用いて、本アルゴリズムとNDTスキャンマッチングによる車両制御結果の比較を行った。場所は本学校内路で行い、高精度3次元地図はMMS(Mobile Mapping System)で計測したものを使用し、LiDARはVelodyne社製VLP-16(データ出力周期 10Hz)を使用した。
(2)評価試験用システムの構成 (略)
(3)車両制御性能の評価
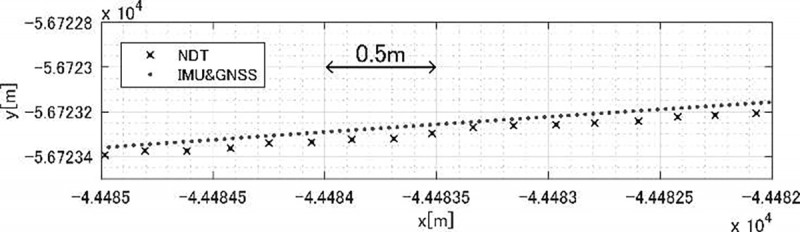
本アルゴリズムとNDTスキャンマッチングによる車両制御結果の比較を行った。車両制御には絶対位置情報が必要となる。本アルゴリズムは相対位置の出力なので、初期位置としてNDTマッチングで推定した絶対位置を使用した。図9に学内路で本アルゴリズムにて車両制御を行った際のそれぞれの手法の位置推定結果の拡大図を示す。
NDTマッチングによる車両制御では、位置推定に数cmのぶれがあることで、ハンドル角の指令値、実測値にもぶれがあることが発生していることが分かる。それに対し本アルゴリズムによる車両制御では、位置推定の連続性が高いことで、ぶれが少なくスムーズに車両制御できることが確認できた。
本アルゴリズムの車両制御適用時の有効性を確認するため、外部ECUから制御を行えるように改造した実験車を用いて、本アルゴリズムとNDTスキャンマッチングによる車両制御結果の比較を行った。場所は本学校内路で行い、高精度3次元地図はMMS(Mobile Mapping System)で計測したものを使用し、LiDARはVelodyne社製VLP-16(データ出力周期 10Hz)を使用した。
(2)評価試験用システムの構成 (略)
(3)車両制御性能の評価
本アルゴリズムとNDTスキャンマッチングによる車両制御結果の比較を行った。車両制御には絶対位置情報が必要となる。本アルゴリズムは相対位置の出力なので、初期位置としてNDTマッチングで推定した絶対位置を使用した。図9に学内路で本アルゴリズムにて車両制御を行った際のそれぞれの手法の位置推定結果の拡大図を示す。
NDTマッチングによる車両制御では、位置推定に数cmのぶれがあることで、ハンドル角の指令値、実測値にもぶれがあることが発生していることが分かる。それに対し本アルゴリズムによる車両制御では、位置推定の連続性が高いことで、ぶれが少なくスムーズに車両制御できることが確認できた。
■ 結言
本研究では、廉価で汎用的なMEMS IMUとマルチGNSS受信機、車輪速センサを組み合わせた自車位置推定アルゴリズムのリアルタイム化を行い、相対位置推定精度の検証と車両制御適用時の評価を行った。本学周辺道路では、100mの走行で0.6m以内の自車の相対位置推定を約95%得られることを確認した。また、車両制御適用時にも目標コースを追従することができ、NDTマッチングと比較しスムーズな制御を行うことができることを確認した。
今後このような技術をNDTマッチングなどと統合し、より廉価なシステム構成で高性能な自車位置推定を実現することを目指す。
今後このような技術をNDTマッチングなどと統合し、より廉価なシステム構成で高性能な自車位置推定を実現することを目指す。
-
 指導教員からのコメント
自動運転・運転支援研究室教授 井上 秀雄
指導教員からのコメント
自動運転・運転支援研究室教授 井上 秀雄
- 自動運転の要となる自己位置推定技術に関する研究です。現在、一般に使われる技術は、①高価スキャンLidarと高精度3D地図によるNDTマッチング技術。②高精度IMUとGNSSを組合わせた複合航法。更には、①+②の技術など、どれも大変超高価な組合せで実用化には向きません。本研究では、廉価なMEMS IMUとGNSS受信機と車両センサを使う、新たな信号処理アルゴリズムにより、高精度だけでなくリアルタイム性に優れた自己位置推定技術を可能にしました。これによりNDTマッチングだけでは、ギクシャクしていた従来の操舵自動制御に比べ、本技術は精度の良いスムーズな操舵制御となりました。この關野君の粘り強い研究成果の実用化が、今後、期待されます。
-
 修士研究学生からの一言
關野 修
修士研究学生からの一言
關野 修
- 実車を用いた実験を行うためには、単にアルゴリズムをシミュレーションして研究するだけではなくて、実際のセンサからの情報をリアルタイムに処理して計算させていくような実装や、実験車を自動運転させるためにその他の必要な要素を含めてシステム全体を作っていく必要があります。そのすべての要素が大学にあったのでこの研究を行うことができ、研究に関係することだけではない様々な知識を身に付けることができました。
- 創造工学部自動車システム開発工学科(大学サイト )
- 教員紹介ページ(大学サイト )
- 研究室ナビ(大学サイト)


