卒業研究のご紹介
2021年版
機械・自動車・ロボット系所属学生
共同非圧縮性流体の中心差分法によるCFDプログラムの開発とその検証
佐藤 佑樹(代表者)静岡県
工学部機械工学科機械工学コース
2021年3月卒業
2021年3月卒業
静岡県立沼津西高等学校出身
長井 理矩群馬県
工学部機械工学科機械工学コース
2021年3月卒業
2021年3月卒業
群馬県立前橋工業高等学校出身
研究の目的
コンピュータで流体の動きをシミュレーションするプログラムを作成し、色々な流れに適用して、うまく計算できるかを調べています。
円管中の流れについて、レイノルズ数(慣性力と粘性力の比を表す単位のない量)が2300よりも小さなときは、外乱があっても層流という乱れのない流れになると教科書には書かれています。
私たちのプログラムで外乱を与えながら計算をすると、レイノルズ数が1500未満時は、確かに乱れのない層流状態が維持されました。ところが1500を超えると、解が不安定になって、発散してしまいました。これは私たちのプログラムに問題があるのか?
これを調べるために、実験装置を組み立てて実験を行い、プログラムによる計算結果と実験結果が一致するかの確認をしました。
円管中の流れについて、レイノルズ数(慣性力と粘性力の比を表す単位のない量)が2300よりも小さなときは、外乱があっても層流という乱れのない流れになると教科書には書かれています。
私たちのプログラムで外乱を与えながら計算をすると、レイノルズ数が1500未満時は、確かに乱れのない層流状態が維持されました。ところが1500を超えると、解が不安定になって、発散してしまいました。これは私たちのプログラムに問題があるのか?
これを調べるために、実験装置を組み立てて実験を行い、プログラムによる計算結果と実験結果が一致するかの確認をしました。
研究内容や成果等
■ 基礎方程式

■ 円管内層流における安定性
十分に発達した円管内層流の直径の10倍の流れ方向の長さの範囲について、解の安定性について調べた。計算領域として40×40×400個の立方体のセルを使用し、それに含まれる最大の円筒形を計算領域とした。最初に各セルの中心位置の速度、圧力に円管内層流の理論解の値を与え、入り口断面の速度分布、出口断面の圧力分布は維持したままで、(1)式、(3)式を繰り返し計算して、解が発散せずに計算し続けられるかどうかを調べた。長さは円管内径Dで、速度は平均流速Uで、圧力はρU2で、時間はD/Uで無次元化した(T=t/(D/U))。時間ステップを0.001とし、κの値を900として計算を行った。
(1)T=0.1 毎に速度分布に±0.5%のホワイトノイズを加えた場合の安定性
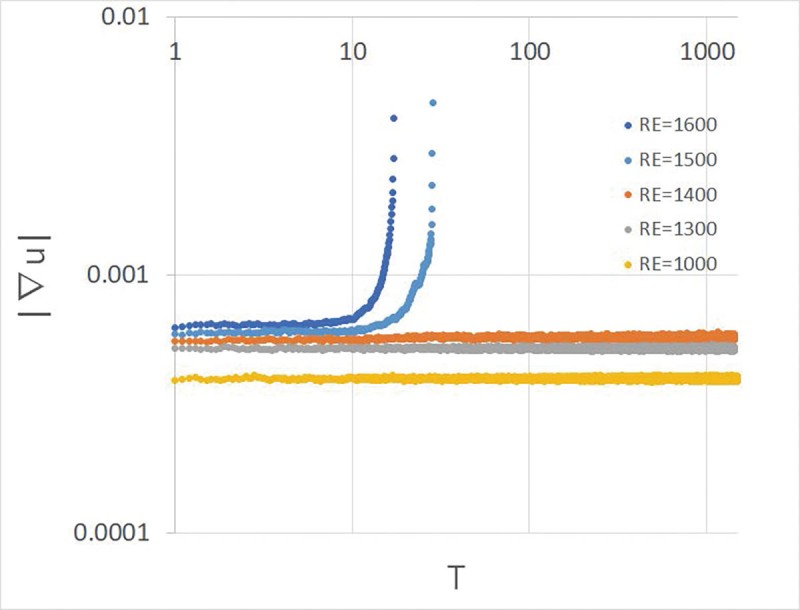
T=0.1毎に、流体領域のすべての点において、速度の各成分の値に-0.005〜0.005の乱数をかけて、各成分に加えた。図1は横軸にTを、縦軸にホワイトノイズを与える直前の|∇u|の値をとった。レイノルズ数が1500以上では,縦軸の値は、しばらくは一定を保つものの、徐々に増加して解は発散した。レイノルズ数が1400以下では、縦軸の値はほぼ一定の値を保って発散することはなかった。
(1)T=0.1 毎に速度分布に±0.5%のホワイトノイズを加えた場合の安定性
T=0.1毎に、流体領域のすべての点において、速度の各成分の値に-0.005〜0.005の乱数をかけて、各成分に加えた。図1は横軸にTを、縦軸にホワイトノイズを与える直前の|∇u|の値をとった。レイノルズ数が1500以上では,縦軸の値は、しばらくは一定を保つものの、徐々に増加して解は発散した。レイノルズ数が1400以下では、縦軸の値はほぼ一定の値を保って発散することはなかった。
(2)一度だけ速度分布に±50%のホワイトノイズを加えた場合の安定性
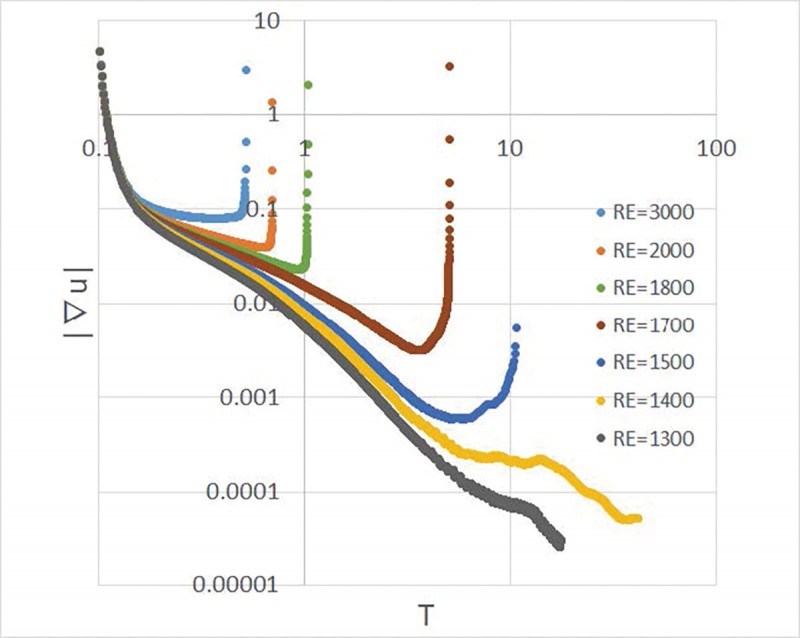
流体領域のすべての点において、速度の各成分の値に-0.5〜0.5の乱数をかけて、各成分に加えて計算を続けた。図2は横軸にTを、縦軸に|∇u|の値をとった。レイノルズ数が 1500以上では、縦軸の値は一旦減少するものの、再度増加して解は発散した。レイノルズ数が1400以下では、縦軸の値は減少を続け発散しなかった。
(3)解発散の意味
レイノルズ数が1500以上で解は発散したが、これは乱流に遷移したことを意味するものではなく、差分法では追随できない大きな乱れに発展したことを意味するに過ぎない。従来の実験的研究によればレイノルズ数が2300以下では、初期の乱れが大きくても層流を保つとされている。その中でも、流線にほとんど乱れがない層流と、層流ではあるが流線が大きく乱れる場合があるのではないかと考えられるので、実験により確かめることとした。
流体領域のすべての点において、速度の各成分の値に-0.5〜0.5の乱数をかけて、各成分に加えて計算を続けた。図2は横軸にTを、縦軸に|∇u|の値をとった。レイノルズ数が 1500以上では、縦軸の値は一旦減少するものの、再度増加して解は発散した。レイノルズ数が1400以下では、縦軸の値は減少を続け発散しなかった。
(3)解発散の意味
レイノルズ数が1500以上で解は発散したが、これは乱流に遷移したことを意味するものではなく、差分法では追随できない大きな乱れに発展したことを意味するに過ぎない。従来の実験的研究によればレイノルズ数が2300以下では、初期の乱れが大きくても層流を保つとされている。その中でも、流線にほとんど乱れがない層流と、層流ではあるが流線が大きく乱れる場合があるのではないかと考えられるので、実験により確かめることとした。
■ 円管内層流の可視化実験
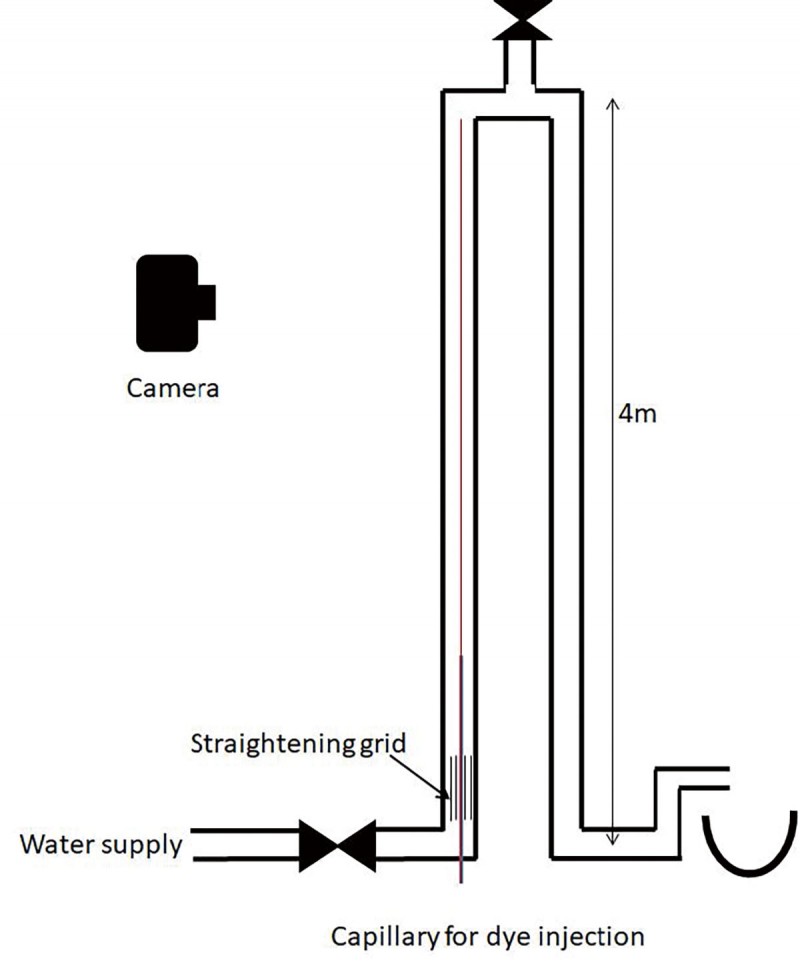
図3に示すような長さ4m内径11mmの透明塩ビパイプを鉛直に立てて、水道を流量調整バルブ、整流格子を介して、曲がりなどにより生じる大きな構造の乱れを取り除いた後に、塩ビパイプに導いた。塩ビパイプ入り口から300mmの位置で、内径0.3mmのステンレスパイプから朱墨を奥の壁面に沿わせて流出させて、流れを可視化した。朱墨の流出直後から管出口近傍までの数点において動画撮影して、流線の状態を観察した。図4レイノルズ数960〜1956までの流れ模様を示す。1が付してある図はステンレスパイプから朱墨が流出直後、4が付してある図は約2m下流の流れ模様である。レイノルズ数が1400以下では流線の乱れはなく、上流下流ともに朱の太い線として流線が観察されたが、レイノルズ数が1500以上になるとステンレスパイプ流出直後に乱れが観察され、下流では朱墨が分散されて薄い線となって観察された。

■ 結言
Navier-Stokesの運動方程式を差分化して前進法で流れ場を解析するにあたり、速度の湧き出しの時間変化がゼロとなるように、圧力分布を決定しながら、次の速度分布を求めた。この際速度の湧き出しが値をもっても、すぐに消滅するような効果を持つ項を関係式に付加した。
この計算手法を用いて、速度分布に乱れを加えながら、円管内層流の解の安定性について調べた結果、レイノルズ数が1500以上では解は発散してしまうが、1400以下では発散せず計算を続けることがわかった。一方鉛直透明パイプを用いて流れの可視化を行い、流線の揺らぎを観察した。その結果レイノルズ数が1400以下では流線の乱れはないが、1500以上になると流線の乱れが発生することが観察された。レイノルズ数が1500以上で解が発散したのは、流れが乱流になることを意味するものではなく、差分法では追随できない大きな乱れが生じることを意味していることがわかった。
この計算手法を用いて、速度分布に乱れを加えながら、円管内層流の解の安定性について調べた結果、レイノルズ数が1500以上では解は発散してしまうが、1400以下では発散せず計算を続けることがわかった。一方鉛直透明パイプを用いて流れの可視化を行い、流線の揺らぎを観察した。その結果レイノルズ数が1400以下では流線の乱れはないが、1500以上になると流線の乱れが発生することが観察された。レイノルズ数が1500以上で解が発散したのは、流れが乱流になることを意味するものではなく、差分法では追随できない大きな乱れが生じることを意味していることがわかった。
-
 卒業研究学生からの一言
佐藤 佑樹
卒業研究学生からの一言
佐藤 佑樹
- 本学の講義では、早い段階で工作機械や溶接の体験学習、製図の勉強などに取り組むカリキュラムとなっており、普通科高校出身者の私にとって非常に取り組みやすかったです。座学では、入学直後に学ぶ数学の知識などが後々に専門分野でも活用できたりと、すべての科目に繋がりがあることを痛感しました。座学で学んだことを総動員させて取り組む実験科目では、知識だけだったものを実際に体感できます。また、実験は毎週のようにあり、実験ごとにレポートを書くのですが、ここで学ぶ点は多く、実験の取り組み方や報告書の書き方は卒業研究でも活かせたと感じています。
- 工学部機械工学科(大学サイト )
- 教員紹介ページ(大学サイト )
- 研究室ナビ(大学サイト)


